Una ecuación indeterminada es una ecuación para la cual hay un conjunto infinito de soluciones – por ejemplo, 2x = y. Las ecuaciones indeterminadas no siempre pueden ser resueltas directamente con la información dada. Por ejemplo, las ecuaciones
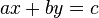

donde a, b, c, y P son enteros (siempre que P no es un número cuadrado), son ecuaciones indeterminadas. Una ecuación donde las variables sólo pueden tomar valores enteros se conoce como una ecuación diofántica, por lo que las anteriores son ejemplos de ecuaciones diofánticas indeterminadas.
Existen ecuaciones que no se pueden resolver mediante los métodos vistos hasta ahora, debido a que poseen mas de una variable y al despejar, simplemente nos queda una variable en función de la otra.
6m = 18n +30 de donde m = 3n +5 ó n = (m - 5)/3
En estos casos cada valor que se le asigne a una variable dará un grupo único de raíces como respuesta para la otra variable.
Si n = 5 m = 20
Si n = 5/3 m = 0
Si n = -2 m = -1
Y así se pueden dar una cantidad infinita de valores de una variable y su respectiva raíz como respuesta para la otra y todos estos pares satisfacen la ecuación
Resolución de ecuaciones indeterminadas
Se trata de encontrar un grupo de posibles respuestas que cumplan ciertas características, por ejemplo si restringimos las posibles soluciones para que sean únicamente positivas y enteras, entonces las únicas respuestas de la ecuación y = 3 - x serán:
x = 1 y = 2
x = 2 y = 1
y cualquier valor de x que sea menor o igual a cero
Esto debido a que cualquier valor mayor de tres dará como resultado un “y” negativo y no se cumpliría la restricción, y con x = 3 el resultado de “y” será 0 y cero no es un numero positivo.
Así se dice que en esta ecuación “y” es igual a un entero positivo siempre que x sea un entero y x <3,>
Para encontrar definitivamente todas las raíces de cada valor de las ecuaciones de dos variables que cumplan con la restricción de ser enteros positivos, se sigue el siguiente método:
- Despejamos la variable con el menor coeficiente.
- En caso de quedar como fracción, descomponemos cada miembro del numerador en cantidades perfectamente divisibles entre el denominador, y las dividimos, nos quedan varias sumas y una fracción mas pequeña.
- Despejamos la fracción resultante, procurando nos quede solo una variable en al menos un miembro.
- Igualamos cada miembro a una nueva variable, la cual es un numero entero.
- Tomando el miembro con una sola de las variables originales, multiplicamos por una cantidad que convierta a el coeficiente de la variable en igual al denominador + 1.
- Repetimos el paso dos, y como para que este resultado nos de entero la fracción tiene que ser un entero, trabajaremos solo con la fracción igualada a la variable que es un entero.
- Despejamos la incógnita original quedando un polinomio en función de la variable entera.
- Sustituimos este polinomio por la variable desconocida en la ecuación original y despejamos la otra variable desconocida.
- Ahora nos quedan dos ecuaciones en función de la nueva variable, sustituimos esta variable por valores enteros a partir del cero, primero los positivos y luego los negativos.
- Cuando el resultado de alguna de las variables resulte negativo nos detenemos, tanto en los positivos como en los negativos, este es intervalo solución.
No hay comentarios:
Publicar un comentario