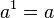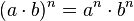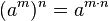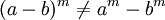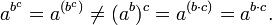martes, 6 de octubre de 2009
lunes, 5 de octubre de 2009
potenciacion
La potenciación no es una operación matemática,es una ley que se nota como an, y que se lee "a elevado a n", que involucra dos números: la base a y el exponente n. Su definición varía según el conjunto numérico al que pertenezca el exponente:
- Cuando el exponente es un número natural, la potenciación corresponde a una multiplicación de varios factores iguales: el exponente determina la cantidad de veces que la base se multiplica por sí misma. Por ejemplo:
 . En general:
. En general:
- cuando el exponente es un entero negativo -p, una potencia que tenga exponente negativo es el resultado de elevar la fracción inversa de la base 1/a al exponente positivo p.
- cuando el exponente es una fracción irreducible m/n, se define
La definición de potenciación puede extenderse a exponentes reales, complejos o incluso matriciales.
Como caso especial, destacar que cualquier número (salvo el 0) elevado a 0 da 1. El caso particular de 00, en principio, no está definido (ver en Cero). Sin embargo, también se puede definir como 1 si nos atenemos a la idea de producto vacío o simplemente por analogía con el resto de números.
Potencia de exponente 1
Toda potencia de exponente 1 es igual a la base.
ejemplo:
Producto de potencias de igual base
El producto de dos o más potencias de igual base a es igual a la potencia de base a y exponente igual a la suma de los correspondientes exponentes. Se coloca la misma base y se suman los exponentes:
ejemplos:
todo número a la potencia 0 es igual a 1
ejemplos:
5^0 = 1
cociente de potencias de igual base
La división de dos potencias de igual base a es igual a la potencia de base a y exponente igual a la resta de los exponentes respectivos. Se coloca la misma base y se restan los exponentes.
Potencia de un producto
La potencia de un producto de base (a·b) y de exponente "n" es igual a la potencia "A" a la "N" por "b" a la "n". Cada base se multiplica por el exponente.
Potencia de una potencia
La potencia de una potencia de base a es igual a la potencia de base a elevada a la multiplicación de ambos exponentes. Se coloca la misma base y se multiplican los exponentes. Así se obtiene esta potencia
Propiedad distributiva
La potenciación es distributiva con respecto a la multiplicación y a la división, pero no lo es con respecto a la suma ni a la resta.
Es distributiva con respecto a la multiplicación y división:
Propiedades que no cumple la potenciación
No es distributiva con respecto a la adición y sustracción:
No cumple la propiedad conmutativa, exceptuando aquellos casos en que base y exponente tienen el mismo valor o son equivalentes. En general, 
Tampoco se cumple la propiedad asociativa:
Potencia de base 10
Normalmente, las potencias con base 10, por la cantidad que represente el exponente, esa será la cantidad de ceros en el resultado. El resto de la base, para sacar el resultado el número se multiplica por sí mismo cuantas veces indique el exponente. Ejemplo 102=100. 105=100000 con 70
Minimo comun multiplo
El nombre de mínimo común múltiplo está hecho de las partes mínimo, común y múltiplo:
¿Qué es un "múltiplo"?
Los múltiplos de un número son lo que tienes cuando lo multiplicas por otros números (si lo multiplicas por 1,2,3,4,5, etc.) como en las tablas de multiplicar.
Aquí tienes ejemplos:
| Los múltiplos de 3 son 3, 6, 9, 12, 15, 18, 21, etc... |
| Los múltiplos de 12 son 12, 24, 36, 48, 60, 72, etc... |
¿Qué es un "múltiplo común"?
Si tienes dos (o más) números, y miras entre sus múltiplos y encuentras el mismo valor en las dos listas, esos son los múltiplos comunes a los dos números.
Por ejemplo, si escribes los múltiplos de dos números diferentes (digamos 4 y 5) los múltiplos comunes son los que están en las dos listas:
| Los múltiplos de 4 son 4,8,12,16,20,24,28,32,36,40,44,... |
| Los múltiplos de 5 son 5,10,15,20,25,30,35,40,45,50,... |
| ¿Ves que 20 y 40 aparecen en las dos listas? Entonces, los múltiplos comunes de 4 y 5 son: 20, 40 (y 60, 80, etc. también) |
¿Qué es el "mínimo común múltiplo"?
Es simplemente el más pequeño de los múltiplos comunes. En el ejemplo anterior, el menor de los múltiplos comunes es 20, así que el mínimo común múltiplo de 4 y 5 es 20.
Calcular el mínimo común múltiplo
En realidad es muy fácil de hacer. Sólo escribe los múltiplos de los números hasta que encuentres uno que coincida.
Ejemplo 1: encuentra el mínimo común múltiplo de 3 y 5:
| Los múltiplos de 3 son 3, 6, 9, 15, ..., y los múltiplos de 5 son 5, 10, 15, 20, ..., así: |
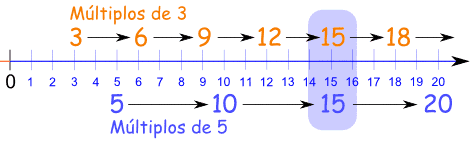 |
| Como puedes ver en esta línea de números, el primer múltiplo que coincide es el 15. Respuesta: 15 |
Y puedes calcular el mínimo común múltiplo de 3 (o más) números.
Ejemplo 2: calcula el mínimo común múltiplo de 4, 6 y 8
| Los múltiplos de 4 son: 4, 8, 12, 16, 20, 24, 28, 32, 36, ... Entonces 24 es el mínimo común múltiplo de (¡no podemos encontrar uno más pequeño!) |
Pista: puedes hacer listas más pequeñas de los números más grandes.
Herramienta para el mínimo común múltiplo
Hay otro método, puedes usar nuestra Herramienta para el mínimo común múltiplo para calcularlo automáticamente.Productos notables y cocientes notables
El cuadrado de la suma de dos cantidades es igual al cuadrado de la primera cantidad más el doble de la primera cantidad por la segunda más el cuadrado de la segunda cantidad.
Cuadrado de la diferencia de dos cantidades
El cuadrado de la suma de dos cantidades es igual al cuadrado de la primera cantidad menos el doble de la primera cantidad por la segunda más el cuadrado de la segunda cantidad.
Producto de la suma por la diferencia de dos cantidades
El producto de la suma por la diferencia de dos cantidades es igual al cuadrado de la primera cantidad menos el cuadrado de la segunda
Cubo de un binomio
El cubo de la suma de dos cantidades es igual al cubo de la primera cantidad mas el triple del cuadrado de la primera por la segunda mas el triple del cuadrado de la segunda por la primera mas el segundo al cubo.
El cubo de la diferencia de dos cantidades es igual al cubo de la primera cantidad menos el triple del cuadrado de la primera por la segunda mas el triple del cuadrado de la segunda por la primera menos el segundo al cubo.
Cocientes Notables
Cociente de la diferencia de los cuadrados de dos cantidades entre la suma o la diferencia de las cantidades
La diferencia de los cuadrados de dos cantidades divididas entre la suma de las cantidades es igual a la diferencia de las cantidades.
La diferencia de los cuadrados de dos cantidades entre la diferencia de las cantidades es igual a la suma de las cantidades.
Caso 1 - Factor común
Cuando se tiene una expresión de dos o más términos algebraicos y si se presenta algún término común, entonces se puede sacar este término como factor común.
Caso 2 - Factor por agrupación de términos
En una expresión de dos, cuatro, seis o un número par de términos es posible asociar por medio de paréntesis de dos en dos o de tres en tres o de cuatro en cuatro de acuerdo al número de términos de la expresión original. Se debe dar que cada uno de estos paréntesis que contiene dos, o tres o mas términos se le pueda sacar un factor común y se debe dar que lo que queda en los paréntesis sea lo mismo para todos los paréntesis o el factor común de todos los paréntesis sea el mismo y este será el factor común.
Caso 3 - Trinomio cuadrado perfecto
Una expresión se denomina trinomio cuadrado perfecto cuando consta de tres términos donde el primero y tercer términos son cuadrados perfectos (tienen raíz cuadrada exacta) y positivos, y el segundo término es el doble producto de sus raíces cuadradas.
Se extrae la raíz cuadrada del primer y tercer término y se separan estas raíces por el signo del segundo término. El binomio así formado se eleva al cuadrado.
Caso 4 - Diferencia de cuadrados perfectos
Dos cuadrados que se están restando es una diferencia de cuadrados. Para factorizar esta expresión se extrae la raíz cuadrada de los dos términos y se multiplica la resta de los dos términos por la suma de los dos.
Caso especial: Se puede presentar que uno o los dos términos de la diferencia contenga mas de un término.
Caso especial: Se puede dar una expresión de cuatro términos donde tres de ellos formen un trinomio cuadrado perfecto que al ser factorizado y combinado con el cuarto término se convierta en una diferencia de cuadrados, o pueden ser seis términos que formen dos trinomios cuadrados perfectos y al ser factorizados formen una diferencia de cuadrados.
Caso 5 - Trinomio cuadrado perfecto por adición y sustracción
Algunos trinomios no cumplen las condiciones para ser trinomios cuadrados perfectos, el primer y tercer término tienen raíz cuadrada perfecta pero el término de la mitad no es el doble producto de las dos raíces. Se debe saber cuanto debe ser el doble producto y la cantidad que falte para cuadrar el término de la mitad, esta cantidad se le suma y se le resta al mismo tiempo, de tal forma se armara un trinomio cuadrado y factorizado unido con el último término tendremos una diferencia de cuadrados.
Caso especial: factorar una suma de cuadrados, se suma el término que hace falta para formar un trinomio cuadrado perfecto y al mismo tiempo se resta esta misma cantidad, así tendremos un trinomio cuadrado perfecto enseguida una diferencia de cuadrados.
Caso 6 - Trinomio de la forma
![]()
Esta clase de trinomio se caracteriza por lo siguiente:
El primer término tiene como coeficiente 1 y la variable esta al cuadrado.
El segundo término tiene coeficiente entero de cualquier valor y signo y la misma variable.
El tercer término es independiente (no contiene la variable).
Para factorar este trinomio se deben abrir dos factores que sean binomios, y donde el primer término de cada binomio es la variable y el segundo término en cada uno de los factores (paréntesis), son dos números , uno en cada paréntesis de tal forma que la suma de los dos del coeficiente del segundo término del trinomio y la multiplicación de los dos del tercer término del trinomio, el signo del segundo término de cada factor depende de lo siguiente:
- ° Si el signo del tercer término es negativo, entonces uno será positivo y el otro negativo, el mayor de los dos números llevara el signo del segundo término del trinomio y el otro número llevara el signo contrario.
° Si el signo del tercer término es positivo, entonces los dos signos serán iguales (positivos o negativos), serán el signo del segundo término del trinomio.
Caso 7 - Trinomio de la forma
![]()
Este trinomio se diferencia del trinomio cuadrado perfecto en que el primer término puede tener coeficiente diferente de 1.
Se procede de la siguiente forma:
Se multiplica todo el trinomio por el coeficiente del primer término, de esta forma se convierte en un trinomio de la forma:
![]()
y se divide por el mismo coeficiente. Se factoriza el trinomio en la parte superior del fraccionario y se simplifica con el número que esta como denominador.
Caso 8 - Cubo perfecto de binomios
Podemos asegurar que una expresión algebraica es un cubo perfecto si cumple las siguientes condiciones:
- ° Posee cuatro términos
° El primer y cuarto término son cubos perfectos (tienen raíces cúbicas exactas).
° El segundo termino sea el triple del cuadrado de la raíz cúbica del primer término multiplicado por la raíz cúbica del último término.
° El tercer termino sea el triple del cuadrado de la raíz cúbica del último término -multiplicado por la raíz cúbica del primer término.
° Los signos son todos mas o también podría ser positivo el primero y el tercero y negativo el segundo y el cuarto.
Para factorizar un cubo perfecto se forma un binomio y se eleva al cubo, el primer término del binomio es la raíz cúbica del primer término y el segundo término es la raíz cúbica del último término. El signo del segundo término es mas si todos los signos del cubo son mas y es menos si los signos del segundo y cuarto término del cubo son menos.
Caso 9 - Suma o diferencia de cubos perfectos
Su nombre lo indica, se reconoce por ser la suma o la resta de dos cubos. Su solución será dos factores, el primero de ellos es un binomio formado por las dos raíces cúbicas de los términos dados, el segundo factor esta formado por tres términos así: la priemra raíz al cuadrado, la primera raíz por la segunda y la segunda raíz al cuadrado. Los signos pueden ser de dos formas acuerdo a lo siguiente:
![]()
![]()
Caso 10 - Suma o diferencia de dos potencias iguales
Resumamos en la siguiente tabla las posibilidades:
Para an-bn con n = par o impar la factorización será:
![]()
Para an-bn con n = par la factorización será:
![]()
Para an+bn con n = impar la factorización será:
![]()
Teorema del residuo
Teorema del Residuo
Una forma muy útil para determinar los Ceros de un Polinomio ![]() es el Teorema del Residuo, el cual vamos a introducir a continuación.
es el Teorema del Residuo, el cual vamos a introducir a continuación.
Si efectuamos la División Algebraica de un Polinomio
![]()
entre ![]() donde
donde ![]() es un número Independiente de
es un número Independiente de ![]() nos quedaría:
nos quedaría:
3x2 + 2x + 1
 x-2 3x3 – 4x2 – 3x – 4
x-2 3x3 – 4x2 – 3x – 4
-3x3 + 6x2
2x2 – 3x
-2x2 + 4x
x – 4
-x + 2
-2
en donde el Cociente es ![]() y el Residuo es
y el Residuo es ![]()
el Polinomio, entonces, se puede expresar como:
![]()
A continuación, si calculamos ![]() en el ejemplo anterior, (si recordamos
en el ejemplo anterior, (si recordamos ![]() se obtiene sustituyendo 2 por
se obtiene sustituyendo 2 por ![]() en la Función)
en la Función)
![]()
Podemos observar que el valor de ![]() es igual al valor del Residuo que se obtuvo en la División Algebraica esto podría indicar que se trata de una coincidencia sin embargo si se efectúa el mismo procedimiento con varias divisiones de
es igual al valor del Residuo que se obtuvo en la División Algebraica esto podría indicar que se trata de una coincidencia sin embargo si se efectúa el mismo procedimiento con varias divisiones de ![]() entre distintos
entre distintos ![]() se podría comprobar que en todos los casos que
se podría comprobar que en todos los casos que ![]() es igual al residuo
es igual al residuo ![]() lo cual constituye el fundamento del Teorema del Residuo.
lo cual constituye el fundamento del Teorema del Residuo.
TEOREMA DEL RESIDUO
Si se Divide el Polinomio ![]() entre el Binomio
entre el Binomio ![]() donde
donde ![]() es un Número Real, el Residuo es igual a
es un Número Real, el Residuo es igual a ![]()
Teorema del Factor
Tomando como base el Teorema del Residuo, se puede establecer el enunciado de este Teorema que nos será muy útil para determinar los Factores de un Polinomio.
Es importante recordar que al efectuar una División Algebraica, si la División es Exacta el Residuo es igual a Cero.
Radicales
Se llama raíz n-ésima de un número a, y se escribe ![]()
, a un número b que elevado a n dé a.
Ejemplos:

![]()
se llama radical; a, radicando; y n, índice de la raíz.
EXISTENCIA DE RADICALES.
Primera: si a es positivo, ![]()
existe, cualquiera que sea n.
![]()
Segunda: si a es negativo, sólo existen sus raíces de índice impar.

Tercera: salvo que a sea una potencia n-ésima de un número entero o fraccionario,![]()
es un número irracional. Sólo podremos obtener su expresión decimal aproximada.
FORMA EXPONENCIAL DE LOS RADICALES
La raíz n-ésima de un número puede ponerse en forma de potencia:
![]()
Esta nomenclatura es coherente con la definición.
![]()
Es importante familiarizarse con la forma exponencial de los radicales, pues nos permitirá expresarlos y operar cómodamente con ellos.

PROPIEDADES DE LOS RADICALES
Los radicales tienen una serie de propiedades, que debemos conocer y utilizar con soltura. Todas ellas son consecuencia inmediata de conocidas propiedades de las potencias. Veámoslas una a una, estudiando su significado en algunos ejemplos, y viendo sus aplicaciones.
Primera:
![]()
Ejemplos:

Esta propiedad tiene dos importantes aplicaciones:
simplificar radicales tal y como se ha visto en los ejemplos anteriores;
conseguir que dos o más radicales tengan el mismo índice (reducir a índice
común).

Segunda:
![]()
Ejemplos:

Esta propiedad tiene dos aplicaciones importantes:
sacar un factor fuera de la raíz;

de modo contrario, juntar varios radicales en uno solo.
![]()
Tercera:

Ejemplos:

Esta propiedad, junto con la primera y segunda, sirve para poner productos y cocientes de radicales bajo una sola raíz.

Cuarta:
![]()
Ejemplos:
![]()
Quinta:
![]()
Ejemplos:

RADICALES SEMEJANTES
Dos radicales son semejantes cuando tienen el mismo índice y radicando.
Los radicales![]()
y ![]()
son semejantes. Tienen el mismo índice, 2, y el mismo radicando, 3.
![]()
y ![]()
son semejantes. Esto se comprueba sacando factores del radical.
![]()
y![]()
son semejantes. Esto se comprueba sacando factores del radical.

Más ejemplos de radicales semejantes:

OPERACIONES CON RADICALES
La suma o la resta de radicales semejantes es otro radical semejante a los dados, cuyo coeficiente es igual a la suma o la resta de los coeficientes de los radicales sumados o restados.
![]()
Ejemplo:
![]()
Si los radicales no son semejantes, la suma se deja indicada.
Ejemplo:
![]()
El producto de radicales, con el mismo índice, es igual a otro radical cuyo coeficiente y radicando son iguales, respectivamente, a los productos de los coeficientes y radicandos de los factores.
![]()
Ejemplo:
![]()
El cociente de dos radicales con el mismo índice, es igual a otro radical, cuyo coeficiente y radicando son iguales, respectivamente, al cociente de los coeficientes y radicandos de los radicales dividendo y divisor.

Ejemplo:
![]()
La potencia de un radical es igual a otro radical, cuyo coeficiente y radicando están elevados a dicha potencia.
![]()
Ejemplo:
![]()
Es importante observar que al elevar al cuadrado un radical de índice 2, se obtiene el radicando.
![]()
Ejemplo:
![]()
EXPRESIONES FRACCIONARIAS
Al efectuar cálculos con radicales pueden surgir expresiones fraccionarias en las que aparezcan radicales.
Estas expresiones no son números racionales, pues para ello el numerador y el denominador tendrían que ser números enteros.
A estas expresiones las llamaremos expresiones fraccionarias, y verifican las mismas propiedades que los números racionales. Es especialmente importante recordar estas dos:
Primera: dos expresiones fraccionarias son equivalentes si los productos cruzados son iguales.
Segunda: si multiplicamos el numerador y el denominador de una expresión fraccionaria por una misma expresión distinta de cero, se obtiene una expresión fraccionaria equivalente a la primera.
Conclusión
Muchas personas encuentran las matemáticas un tema arduo, complicado y, a veces, indescifrable. Por eso, en esta carpeta hemos tratado de huir de formalismos, que en ocasiones consiguen desviar y hemos ejemplificado todas las definiciones
Las bases de las matemáticas no es saber mucho, sino saber hacer.


![a^{\frac{n}{m}} = \sqrt[m]{a^n}](http://upload.wikimedia.org/math/3/9/8/3983643a5db08e21da69fffabbc0875c.png)