Algebra: potenciacion

La potenciación no es una operación matemática,es una ley que se nota como aⁿ, y que se lee "a elevado a n", que involucra dos números: la base a y el exponente n. Su definición varía según el conjunto numérico al que pertenezca el exponente:

Cuando el exponente es un número natural, la potenciación corresponde a una multiplicación de varios factores iguales: el exponente determina la cantidad de veces que la base se multiplica por sí misma. Por ejemplo: $2^4 = 2 \cdot 2 \cdot 2 \cdot 2 = 16$ . En general:

$a^n = \underbrace{a \times \cdots \times a}_n,$

cuando el exponente es un entero negativo -p, una potencia que tenga exponente negativo es el resultado de elevar la fracción inversa de la base 1/a al exponente positivo p.

$a^{-p}= \frac{1}{a^p}$

cuando el exponente es una fracción irreducible m/n, se define

$a^{\frac{n}{m}} = \sqrt[m]{a^n}$

La definición de potenciación puede extenderse a exponentes reales, complejos o incluso matriciales.

Como caso especial, destacar que cualquier número (salvo el 0) elevado a 0 da 1. El caso particular de 0⁰, en principio, no está definido (ver en Cero). Sin embargo, también se puede definir como 1 si nos atenemos a la idea de producto vacío o simplemente por analogía con el resto de números.

Potencia de exponente 1

Toda potencia de exponente 1 es igual a la base.

$a^1 = a \,$

ejemplo:

$54^1=54 \,$

Producto de potencias de igual base

El producto de dos o más potencias de igual base a es igual a la potencia de base a y exponente igual a la suma de los correspondientes exponentes. Se coloca la misma base y se suman los exponentes:

$a^m \cdot a^n = a^{m + n}$

ejemplos:

$9^3 \cdot 9^2 = 9^{3+2}= 9^5$

todo número a la potencia 0 es igual a 1

ejemplos:

5^0 = 1

cociente de potencias de igual base

La división de dos potencias de igual base a es igual a la potencia de base a y exponente igual a la resta de los exponentes respectivos. Se coloca la misma base y se restan los exponentes.

$\frac{a^m}{a^n}=a^{m - n}$

Potencia de un producto

La potencia de un producto de base (a·b) y de exponente "n" es igual a la potencia "A" a la "N" por "b" a la "n". Cada base se multiplica por el exponente.

$(a \cdot b)^n=a^n \cdot b^n$

Potencia de una potencia

La potencia de una potencia de base a es igual a la potencia de base a elevada a la multiplicación de ambos exponentes. Se coloca la misma base y se multiplican los exponentes. Así se obtiene esta potencia

$(a^m)^n = a^{m \cdot n}$

Propiedad distributiva

La potenciación es distributiva con respecto a la multiplicación y a la división, pero no lo es con respecto a la suma ni a la resta.

Es distributiva con respecto a la multiplicación y división:

$(a \cdot b)^n = a^n \cdot b^n$

$\Big(\frac{a}{b}\Big)^n = \frac{a^n}{b^n}$

Propiedades que no cumple la potenciación

No es distributiva con respecto a la adición y sustracción:

$(a + b)^m \neq a^m + b^m$

$(a - b)^m \neq a^m - b^m$

No cumple la propiedad conmutativa, exceptuando aquellos casos en que base y exponente tienen el mismo valor o son equivalentes. En general, $a^b \neq b^a$

Tampoco se cumple la propiedad asociativa:

$a^{b^c}=a^{(b^c)}\ne (a^b)^c=a^{(b\cdot c)}=a^{b\cdot c}.$

Potencia de base 10

Normalmente, las potencias con base 10, por la cantidad que represente el exponente, esa será la cantidad de ceros en el resultado. El resto de la base, para sacar el resultado el número se multiplica por sí mismo cuantas veces indique el exponente. Ejemplo 102=100. 105=100000 con 70

Algebra

lunes, 5 de octubre de 2009

potenciacion

Potencia de exponente 1

Producto de potencias de igual base

cociente de potencias de igual base

Potencia de un producto

Potencia de una potencia

Propiedad distributiva

Propiedades que no cumple la potenciación

Potencia de base 10

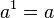
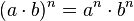
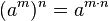
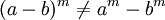
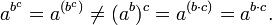
No hay comentarios:

Publicar un comentario

Seguidores

Archivo del blog

Datos personales